Ergodicity & Portfolio Turnover
Will you play this game:
Would you be willing to wager 80% of your entire savings?
Consider the following hint: Expected value of one toss = 0.5 X 1.6 + 0.5 X 0.6 = 1.1 Expected value after 20 tosses = 1.1 ^ 20 = 6.72.
That is if you start with Rs. 100 the expected value of the game after 20 tosses is 672. If you play the game thousands of times, the average amount you that will be left with is Rs. 672 (you can simulate this in an excel – brownie points for anyone who shares the simulation).
Some motivation from Mr. Kipling: “If you can make one heap of all your winnings. And risk it on one turn of pitch-and-toss…”.
This is an extremely risky bet.
There is approximately 42% chance that you lose more than 50% . And about 26% probability that you lose more than 90% of the amount you start with.
Why?
Following is a simulation of 10 players playing this game:
Note the average of all ten is 688 (over large number of simulations this converges to 672). But the average is being dragged up by one instance of 3362 (the lucky one). 4 players have lost money. 2 have lost more than 90%.
In this game, one individual can elevate the overall average, but the longer you play, the less likely it is to encounter such an individual. Additionally, the likelihood of losing all of your wealth over time, even if you win a significant amount in the beginning - is 100%.
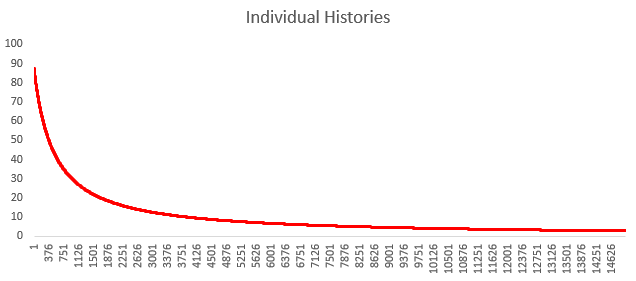
All individual histories - your total winnings, as you keep playing for longer i.e. more than 20 times, would look like this:
Play long enough & you are bound to go broke in this game.
Suppose we modify the game where now you win 70% of your bet and still lose 40% per toss. You might be feeling perplexed or fearful at this point, perhaps both. You probably consider this to be a poor bet. However, this is, in fact, a fantastic bet. All individual trajectories would grow exponentially over time. You should bet heavily and continue to play for as long as possible.
Why?
Consider the first game. Let’s consider two instances. You get HEADS (H) first & then a TAIL (T). So your 100 becomes 160 and then you lose 40% and end up at 96 Rs. What if you get TH. Then you go to 60 first and then win 60% to end again at 96 Rs. In both instances you end up with less than 100.
In the second game where you have tilted the odds slightly you end up at 102 Rs (170*0.6 or 60*1.7).
In the fist case for both scenarios you end at a value less than you started with and in the second case you end up at a value higher than you started with.
(Simulate in an Excel).
Suppose you have the opportunity to invest in one of the following eight portfolios. Each manager has a 50% chance of correctly identifying a good investment opportunity. However, the portfolio held by these managers have varying downside-upside ratios. And they reinvest everything after each bet. Portfolio A has a 10% downside for bad investments and an 11% upside for good ones. Portfolio H offers a 9x return for right bets, but a 90% loss for bad ones.
Note that the expected value (1-Downside) *(1+Upside) for each of these managers is 1. This is equivalent to our game where after HT or TH you end up with exactly Rs. 100 that you started with.
Most people pick H. But overtime the expected value of what these managers will make is exactly the same.
Now here is the investing bit:
Its easier, conservative & prudent to play the games that are at the top – the low-risk uncertainties. Because you can be sure you got the odds right (why low beta or low volatility is often preferred – more predictability). But most big winners will be at the bottom – with a lot of survivorship bias. These guys will get lot of capital at exactly the wrong time. This is what you need to protect yourself from.
Also since the odds change quickly for manager A rather than managers H – a deep value portfolio will have higher turnover than a growth portfolio.
Strike rates differ. Odds are dynamic. Investing (& life) is hazy. Its not all “math”. But most of it - is.
Averages matter when you can do something repeatedly. Life and investing are single instance journeys.
Protect the downside.